Polynomial Regression Using sklearn Module in Python

Linear regression is one of the most used regression techniques in machine learning. However, linear regression doesn’t work all the time. As an alternative to linear regression, we can use polynomial regression. In this article, we will discuss polynomial regression. We will also implement polynomial regression using sklearn in Python.

What is Polynomial Regression?

Polynomial regression is a regression algorithm that we use to model non-linear data. When we have a dataset that contains non-linear data, we cannot use linear regression or multiple regression. In such a case, we can use polynomial regression. 

In polynomial regression, we fit a polynomial equation Y= A0+A1X+ A2X^2+ A3X^3+ A4X^4 +... ANX^N such that for any entry (Xi, Yi) in the dataset, Y_i is closest to A0+A1Xi+ A2Xi^2+ A3Xi^3+ A4Xi^4 +... ANXi^N.

Here, N is called the degree of the polynomial. It is chosen in such a way that the polynomial gives accurate results. At the same time, it shouldn’t also cause over-fitting. 

Linear Regression vs Polynomial Regression

As I said, polynomial regression is an alternative to linear regression. Therefore, we must compare why polynomial regression is better than linear regression in some cases.

To discuss this, consider the following dataset. 

x	y
30	110
40	105
50	120
60	110
70	221

If you fit a linear regression line for this dataset, you will get the regression line as shown in the following image.

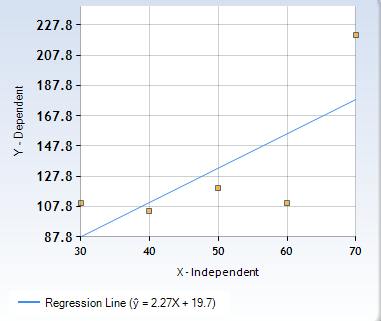
Here, you can see that some of the data points are very far from the regression line. Thus, the regression line will give inaccurate results for our dataset.

Now, if we fit a polynomial regression line of degree 3 using the same dataset, the regression line comes out as shown in the following image. 

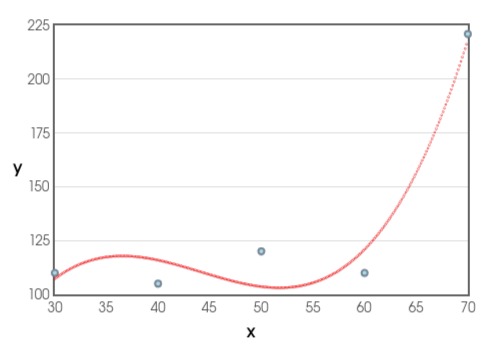
Here, you can see that the regression line fits the data accurately. It also doesn’t cause over-fitting and we can get accurate results for the dataset using this regression line. 

Thus, whenever we have a dataset in which the independent variables and the dependent variables are related non-linearly, we can use polynomial regression.

Implement Polynomial Regression Using sklearn in Python

To implement polynomial regression, we will use the linear regression technique. However, we will prepare our data in a way that the linear regression model will give us an equation for a polynomial. 

For instance, if we have a variable X and we have to fit a polynomial of degree 3, we will fit the equation  Y= A0X^0+A1X+ A2X^2+ A3X^3. Here, for each pair (X_i, Y_i) in the training set, we will calculate the values X^0, X, X^2, and X^3. Now, we will create the vector (Xi^0, Xi, Xi^2, Xi^3) in the place of X_i. Thus, we have transformed the equation of a single independent variable into four independent variables. 

After this, we will use the multiple regression analysis to find A₀, A₁, A₂, and A₃ that will generate our polynomial equation. To implement polynomial regression using sklearn in Python, we will use the following steps.

• First, we will use the PolynomialFeatures() function to create a feature matrix. The PolynomialFeatures() function takes the required degree of the polynomial as its input argument and returns a new feature matrix consisting of all polynomial combinations of the features with a polynomial degree less than or equal to the specified degree.
• After this, we will use the fit_transform() method to properly scale the input data. In polynomial regression, we deal with the powers of the variable. Therefore, it is necessary to perform data preprocessing and transform the data. The fit_transform() method, when invoked on the PolynomialFeatures object returned by the PolynomialFeatures() function, calculates the mean and variance of the data and transforms it using the mean and variance. After execution, it returns the processed data. 
• Now, we will fit the PolynomialFeatures object using the fit() method. The fit() method, when invoked on a PolynomialFeatures object returned by the PolynomialFeatures() function, takes the vector containing the independent variables as its first argument and a vector containing the dependent variable as its second input argument. After execution, it returns the fitted PolynomialFeatures object.

After creating the PolynomialFeatures object, we will implement polynomial regression using the LinearRegression() function defined in the sklearn module in Python. For this, we will use the following steps.

• First, we will import the LinearRegression() function from the sklearn module using the import statement.
• After importing, we will create a LinearRegression model. For this, we will use the LinearRegression() function. The LinearRegression() function returns a LinearRegression model after execution.
• Once we create the LinearRegression model, we will fit our data into the linear regression model. For this, we will use the fit() method. The fit() method takes the list containing independent variables as its first input argument and the list containing the dependent variable as its second input argument. We will pass the vector returned by the fit_transform() method as the first input argument and the list of independent variables as the second input argument to the fit() method.
• After execution, the fit() method returns a fitted linear regression model.
• To access the coefficient of the independent variable in the fitted linear regression model, you can use the coef_ attribute. 
• To access the constant term in the linear regression equation, you can use the intercept_ attribute of the linear regression model.

The entire program to implement polynomial regression using the sklearn module in Python is as follows.

from sklearn.preprocessing import PolynomialFeatures
import numpy
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
x= [30,40,50,60,70]
y=[110,105,120,110,221]
X= numpy.array(x).reshape(-1,1)
polynomial_feature=PolynomialFeatures(degree=3)
z=polynomial_feature.fit_transform(X)
polynomial_feature.fit(z,y)
linear_model=LinearRegression()
trained_model=linear_model.fit(z,y)
coefficients=[float(t) for t in trained_model.coef_]
intercept=float(trained_model.intercept_)
print("The coefficients are:",coefficients)
print("The intercept is:",intercept)

Output:

The coefficients are: [0.0, 47.747619049162914, -1.114642857173089, 0.008416666666860806]
The intercept is: -549.2285714542302

Here, the coefficients of X^0, X, X^2, and X^3 are 0, 47.747619049162914, -1.114642857173089, and 0.008416666666860806 respectively. Similarly, the intercept is -549.2285714542302.

If we plot the predicted values and the actual values of the data, the output graph looks as shown in the following example.

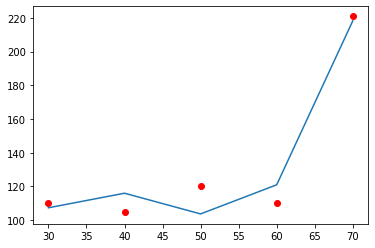
Here, the blue line shows the polynomial predicted by the implemented polynomial regression equation. The red points are the original data points.

Hence, you can observe that we have successfully implemented polynomial regression in Python using the LinearRegression() and PolynomialFeatures() function in the sklearn module in Python. 

Advantages of Polynomial Regression

The main advantage of polynomial regression is that we can use it in place of linear regression if the data is not linear. In other words, we can model analyze non-linear datasets, and predict relationships between variables.

Additionally, you can control over-fitting and under-fitting in the machine learning model by increasing or decreasing the degree of the polynomial.

Disadvantages of Polynomial regression

The major disadvantages of polynomial regression include the following.

Polynomial regression is extremely sensitive to outliers. Therefore, even a single outlier affects the model significantly producing inaccurate results. Therefore, you should make sure to remove all the outliers while data cleaning. 

Increasing the degree of polynomial regression causes over-fitting. So, to avoid over-fitting, we need to perform the hit and trial method to find the best degree for the polynomial. This might frustrate you a bit. 

Conclusion

In this article, we have discussed polynomial regression and its implementation using the sklearn module in Python. Polynomial regression is used in many applications such as tissue growth rate prediction, death rate prediction, speed regulation software, etc.

As you can observe from the implementation, polynomial regression is just a modification of linear regression where we use a feature matrix of powers of the independent variables instead of just the variables to train the machine learning model. However, it enables us to analyze non-linear datasets that can never be analyzed correctly using a simple linear regression model or multiple regression analysis models.

I hope you enjoyed reading this article. To learn more about programming, you can read this article on dynamic role based authorization using ASP.net. You can also read this article on user activity logging using Asp.net.