Hierarchical Clustering: Applications, Advantages, and Disadvantages
Hierarchical clustering is an unsupervised machine-learning algorithm used to group data points into clusters. In this article, we will discuss the basics of hierarchical clustering, its advantages, disadvantages, and applications in real-life situations.
What is Hierarchical Clustering?
Hierarchical clustering is an unsupervised machine learning algorithm used to group data points into various clusters based on the similarity between them. It is based on the idea of creating a hierarchy of clusters, where each cluster is made up of smaller clusters that can be further divided into even smaller clusters. This hierarchical structure makes it easy to visualize the data and identify patterns within the data.
Hierarchical clustering is of two types.
- Agglomerative clustering
- Divisive clustering
What is Agglomerative Clustering?
Agglomerative clustering is a type of data clustering method used in unsupervised learning. It is an iterative process that groups similar objects into clusters based on some measure of similarity. Agglomerative clustering uses a bottom-up approach for dividing data points into clusters. It starts with individual data points and merges them into larger clusters until all of the objects are clustered together.
The algorithm begins by assigning each object to its own cluster. It then uses a distance metric to determine the similarity between objects and clusters. If two clusters have similar elements, they are merged together into a larger cluster. This continues until all objects are grouped into one final cluster. For example, consider the following image.
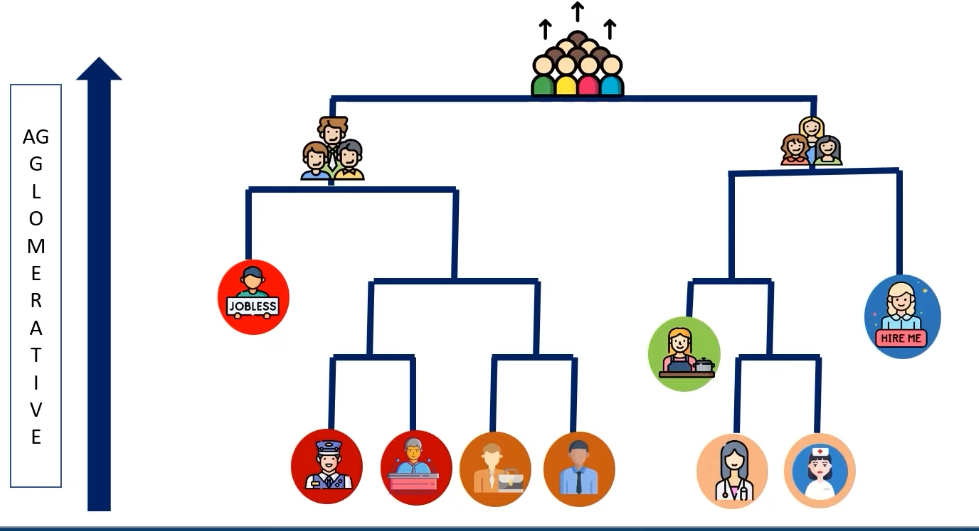
- In this image, a population has been clustered into different clusters. The individual persons are assigned their own cluster at the bottom.
- As we move upwards, the clusters are merged to form bigger clusters. For instance, the male and employed people are clustered together and jobless male persons are put into a different cluster. These clusters are then grouped together to form a cluster representing all the males.
- Similarly, The individual females are assigned their own cluster at the bottom. As we move upwards, the clusters are merged to form bigger clusters. For instance, the female employed people are clustered together and jobless females are put into a different cluster. These clusters are then grouped together to form a cluster representing all the females.
- At the top, the clusters representing males and females are merged to form a single cluster representing the entire population.
The advantage of agglomerative clustering over other techniques is that it can handle large datasets effectively, as it only requires comparisons between pairs of objects or clusters. This makes it relatively efficient for large datasets.
What is Divisive Clustering?
Divisive clustering is also a type of hierarchical clustering that is used to create clusters of data points. It is an unsupervised learning algorithm that begins by placing all the data points in a single cluster and then progressively splits the clusters until each data point is in its own cluster. Divisive clustering is useful for analyzing datasets that may have complex structures or patterns, as it can help identify clusters that may not be obvious at first glance.
Divisive clustering works by first assigning all the data points to one cluster. Then, it looks for ways to split this cluster into two or more smaller clusters. This process continues until each data point is in its own cluster. For example, consider the following image.
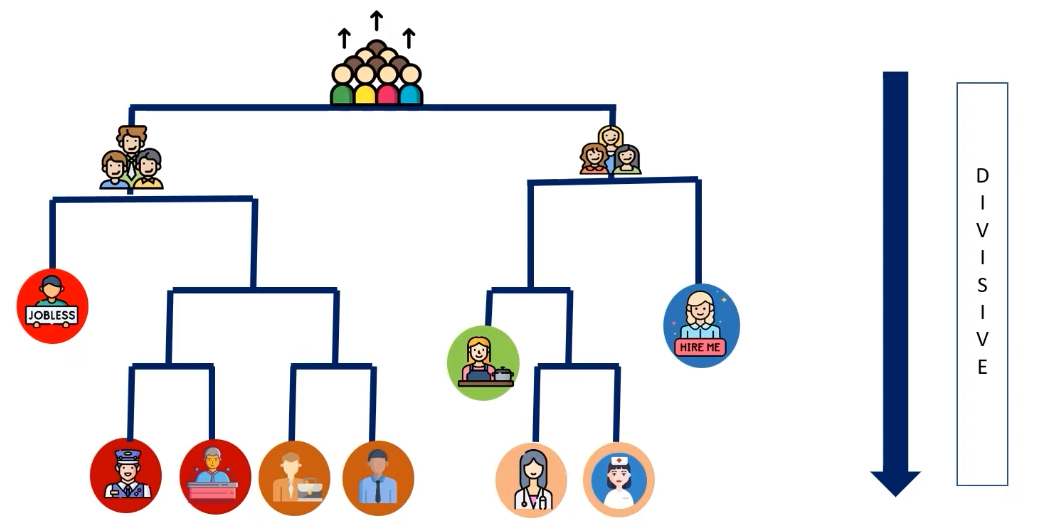
- In the given example, the divisive clustering algorithm first considers the entire population as a single cluster. Then, it divides the population into two clusters containing males and females.
- Next, the algorithm divides the clusters containing males and females on the basis of whether they are employed or unemployed.
- The algorithm keeps dividing the clusters into smaller clusters until it reaches a point where the clusters consist of a single person.
Advantages of Hierarchical Clustering
Hierarchical clustering is a widely used technique in data analysis, which involves the grouping of objects into clusters based on their similarity. This method of clustering is advantageous in a variety of ways and can be used to solve various types of problems. Here are 10 advantages of hierarchical clustering:
- Robustness: Hierarchical clustering is more robust than other methods since it does not require a predetermined number of clusters to be specified. Instead, it creates hierarchical clusters based on the similarity between the objects, which makes it more reliable and accurate.
- Easy to interpret: Hierarchical clustering produces a tree-like structure that is easy to interpret and understand. This makes it ideal for data analysis as it can provide insights into the data without requiring complex algorithms or deep learning models.
- Flexible: Hierarchical clustering is a flexible method that can be used on any type of data. It can also be used with different types of similarity functions and distance measures, allowing for customization based on the application at hand.
- Scalable: Hierarchical clustering is a scalable method that can easily handle large datasets without becoming computationally expensive or time-consuming. This makes it suitable for applications such as customer segmentation where large datasets need to be processed quickly and accurately.
- Visualization: Hierarchical clustering produces a visual tree structure that can be used to gain insights into the data quickly and easily. This makes it an ideal choice for exploratory data analysis as it allows researchers to gain an understanding of the data at a glance.
- Versatile: Hierarchical clustering can be used for both supervised and unsupervised learning tasks, making it extremely versatile in its range of applications.
- Easier to apply: Since there are no parameters to specify in hierarchical clustering, it is much easier to apply compared to other methods such as k-means clustering or k-prototypes clustering. This makes it ideal for novice users who need to quickly apply clustering techniques with minimal effort.
- Greater accuracy: Hierarchical clustering often tends to produce superior results compared to other methods of clustering due to its ability to create more meaningful clusters based on similarities between objects rather than arbitrary boundaries set by cluster centroids or other parameters.
- Non-linearity: Agglomerative or divisive clustering can handle non-linear datasets better than other methods, which makes it suitable for cases where linearity cannot be assumed in the dataset being analyzed.
- Multiple-level output: By producing a hierarchical tree structure, hierarchical clustering provides multiple levels of output which allows users to view data at different levels of detail depending on their needs. This flexibility makes it an attractive choice in many situations where multiple levels of analysis are required.
Disadvantages of Hierarchical Clustering
While hierarchical clustering is a powerful tool for discovering patterns and relationships in data sets, it also has its drawbacks. Here are 10 disadvantages of hierarchical clustering:
- It is sensitive to outliers. Outliers have a significant influence on the clusters that are formed, and can even cause incorrect results if the data set contains these types of data points.
- Hierarchical clustering is computationally expensive. The time required to run the algorithm increases exponentially as the number of data points increases, making it difficult to use for large datasets.
- The results of Agglomerative or divisive clustering can sometimes be difficult to interpret the results due to its complexity. The dendrogram representation of the clusters can be hard to understand and visualize, making it difficult to draw meaningful conclusions from the results.
- It does not guarantee optimal results or the best possible clusterings. Since it is an unsupervised learning algorithm, it relies on the researcher’s judgment and experience to assess the quality of the results.
- Hierarchical clustering methods require a predetermined number of clusters before they can begin clustering, which may not be known beforehand. This makes it difficult to use in certain applications where this information is not available.
- The results produced by hierarchical clustering may be dependent on the order in which the data points are processed, making it difficult to reproduce or generalize them for other datasets with similar characteristics.
- The algorithm does not provide any flexibility when dealing with multi-dimensional data sets since all variables must be treated equally in order for accurate results to be obtained.
- Agglomerative or divisive clustering is prone to producing overlapping clusters, where different groups of data points may share common characteristics and thus be grouped together even though they should not belong to the same cluster.
- Hierarchical clustering requires manual intervention for selecting the appropriate number of clusters, which can be time-consuming and prone to errors if done incorrectly or without proper knowledge about the data set being analyzed.
- It cannot handle categorical variables effectively since they cannot be converted into numerical values and thus will fail to produce meaningful clusters if used in hierarchical clustering algorithms.
Applications of Hierarchical Clustering
Hierarchical clustering is a type of unsupervised machine learning that can be used for many different applications. It is used to group similar data points into clusters, which can then be used for further analysis. Here are 10 applications of hierarchical clustering:
- Customer segmentation: Agglomerative or divisive clustering can be used to group customers into different clusters based on their demographic, spending, and other characteristics. This can be used to better understand customer behavior and to target marketing campaigns.
- Image segmentation: Hierarchical clustering can be used to segment images into different regions, which can then be used for further analysis.
- Text analysis: Hierarchical clustering can be used to group text documents based on their content, which can then be used for text mining or text classification tasks.
- Gene expression analysis: Hierarchical clustering can be used to group genes based on their expression levels, which can then be used to better understand gene expression patterns.
- Anomaly detection: Hierarchical clustering can be used to detect anomalies in data, which can then be used for fraud detection or other tasks.
- Recommendation systems: Hierarchical clustering can be used to group users based on their preferences, which can then be used to recommend items to them.
- Risk assessment: Agglomerative or divisive clustering can be used to group different risk factors in order to better understand the overall risk of a portfolio.
- Network analysis: Hierarchical clustering can be used to group nodes in a network based on their connections, which can then be used to better understand network structures.
- Market segmentation: Hierarchical clustering can be used to group markets into different segments, which can then be used to target different products or services to them.
- Outlier detection: Hierarchical clustering can be used to detect outliers in data, which can then be used for further analysis.
Conclusion
Hierarchical clustering is a powerful tool for discovering patterns and relationships in datasets. It can help uncover hidden correlations between variables that would otherwise remain undetected and provide valuable insights into customer behavior or product trends. Despite its drawbacks, hierarchical clustering remains an important tool for data scientists and data analysts looking to gain a better understanding of their datasets.
The choice of distance metric is important for the success of agglomerative or divisive clustering. Common metrics used include Euclidean distance, Manhattan distance, or cosine similarity. Different metrics may produce different results from the same dataset, so it is important to choose the most appropriate metric for the task at hand. It can also be difficult to determine the optimal number of clusters for a dataset with hierarchical clustering. To address this problem, there are several methods available to assess the quality of the clustering result and select the optimal number of clusters automatically. These methods include silhouette coefficient analysis and gap statistics.
I hope you enjoyed reading this article. Stay tuned for more informative articles.
Happy Learning!
