Elbow Method in Python for K-Means and K-Modes Clustering
Partitioning-based clustering algorithms have a major issue. While implementing these algorithms, we don’t know the exact number of clusters to be formed. In this article, we will discuss the elbow method to find the optimal number of clusters in k-means and k-modes clustering algorithms. We will also implement the entire procedure of finding optimal clusters using the elbow method in python.
What is the Elbow Method?
The elbow method is a heuristic used to determine the optimal number of clusters in partitioning clustering algorithms such as k-means, k-modes, and k-prototypes clustering algorithms.
With the increase in the number of clusters, the total cluster variance for a given dataset decreases rapidly. After a point, the total cluster variance becomes almost constant or the rate of decrease in total cluster variance becomes very low. In such a case, when we plot total cluster variance vs the number of clusters, the graph takes a shape of a bent elbow.
The point after which the decrease in cluster variance becomes stagnant is termed the elbow. The point at the elbow is chosen as the optimal number of clusters. Hence the name elbow method.
Elbow Method Implementation Steps in Python
- To implement the elbow method in python, we will take different values for numbers of clusters for the given dataset and perform clustering.
- After training the model, we will calculate the total cluster variance for each value.
- After obtaining the total cluster variance and the number of clusters, we will plot it.
- After plotting the graph for cluster variance vs the number of clusters, we will select the elbow point and use it as the optimal number of clusters.
Elbow Method Implementation For K-Means Clustering in Python
To implement the elbow method for k-means clustering in python, we will use the sklearn module. You can read this article on k-means clustering with the sklearn module in python to learn how to perform k-means clustering with a given dataset. You can also read this article on k-means clustering with a numerical example to get a better understanding of the k-means clustering algorithm.
Following are the steps to implement the elbow method to find the best k for k-means clustering.
- First, we will create a python dictionary named
elbow_scores. In the dictionary, we will store the number of clusters as keys and the total cluster variance of the clusters for the number associated value. - Using a for loop, we will find the total cluster variance for each k in k-means clustering. We will take the values of k between 2 to 10. You can choose any range after data preprocessing and analyzing it for the probable number of clusters in the dataset.
- Inside the for loop, we will first create an untrained machine-learning model for k-means clustering using the
KMeans()function in the sklearn module. - After creating the untrained model, we will train it using the given dataset using the
fit()method. - After training the machine learning model, we will calculate the total cluster variance for current clusters. For this, we will use the
inertia_attribute of the trained machine learning model. We will store the current number of clusters and the total cluster variance in theelbow_scoresdictionary as key-value pairs. - Finally, we will plot the total cluster variance and number of clusters and find the elbow point. After finding the elbow point, you can use the number as the best k for k-means clustering.
The entire process for implementing the elbow method in python for k-means clustering is shown below.
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
training_data=[(2,10),(2,6),(11,11),(6,9),(6,4),(1,2),(5,10),(4,9),(10,12),(7,5),(9,11),(4,6),(3,10),(3,8),(6,11)]
elbow_scores = dict()
range_of_k = range(2,10)
for k in range_of_k :
untrained_model = KMeans(n_clusters=k)
trained_model=untrained_model.fit(training_data)
elbow_scores[k]=trained_model.inertia_
plt.plot(elbow_scores.keys(),elbow_scores.values())
plt.scatter(elbow_scores.keys(),elbow_scores.values())
plt.xlabel("Values of K")
plt.ylabel("Sum of squared distances")
plt.show()Output
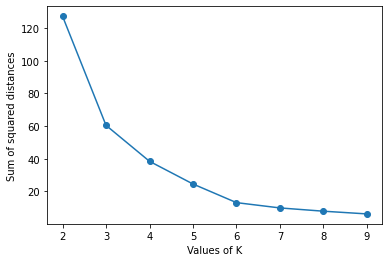
In the above plot, k=3 or k=4 can be the optimal number of clusters in the dataset. This is a drawback of the elbow method that we are not able to identify exactly what should be the optimal number of clusters. This is due to the reason that we try to observe it visually and the slope of the plot cannot always have a drastic change. The approach using the Silhouette coefficient to find the optimal number of clusters in the dataset doesn’t have any such drawback.
Elbow Method Implementation For K-Modes Clustering in Python
Just like k-means clustering, the k-modes clustering algorithm is a partitioning-based clustering algorithm. We can also use the elbow method to find the optimal number of clusters for k-modes clustering.
To implement the elbow method for k-modes clustering in python, we will use the kmodes module. You can read this article on k-modes clustering for categorical data in python to learn how to perform k-modes clustering with a given dataset. You can also read this article on k-modes clustering with a numerical example to get a better understanding of the k-modes clustering algorithm.
Following are the steps to implement the elbow method to find the best k for k-means clustering.
- We will create a python dictionary named
elbow_scores. In the dictionary, we will store the number of clusters as keys and the total cluster variance of the clusters for the number associated value. - Using a for loop, we will find the total cluster variance for each k in k-modes clustering. We will take the values of k between 2 to 8. You can choose any range after data preprocessing and analyzing it for the probable number of clusters in the dataset.
- Inside the for loop, we will first create an untrained machine-learning model for k-modes clustering using the
KModes()function in the kmodes module. - After creating the untrained model, we will train it using the given dataset using the fit() method.
- After training the machine learning model, we will calculate the total cluster variance for current clusters. For this, we will use the
cost_attribute of the trained machine learning model. We will store the current number of clusters and the total cluster variance in theelbow_scoresdictionary as key-value pairs. - Finally, we will plot the total cluster variance and number of clusters and find the elbow point. After finding the elbow point, you can use the number as the best k for k-modes clustering.
The entire process for implementing the elbow method in python for k-modes clustering is shown below.
from kmodes.kmodes import KModes
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data=pd.read_csv("KModes-dataset.csv", index_col=["Student"])
elbow_scores = dict()
K = range(2,10)
for k in K:
untrained_model=KModes(n_clusters=k, n_init=4)
trained_model=untrained_model.fit(data)
elbow_scores[k]=trained_model.cost_
plt.plot(elbow_scores.keys(),elbow_scores.values())
plt.scatter(elbow_scores.keys(),elbow_scores.values())
plt.xlabel("Values of K")
plt.ylabel("Total Cluster Variance")
plt.show()Output:
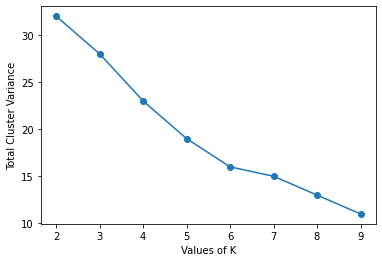
In this example, you can observe that the chart doesn’t have a sharp elbow point. In the output image, At K=6, we get an elbow-like structure. However, the rate of decrease in cluster variance is significant even after this point. K=6 might be the optimal number of clusters. However, we cannot rely on this analysis completely.
In these cases, the elbow method to find the optimal number of clusters fails. As an alternative, you can use the silhouette coefficient approach to find the optimal number of clusters for k-modes clustering.
Elbow Method Implementation For K-Prototypes Clustering in Python
We can also use the elbow method to find the best k for k-prototypes clustering. It is also a partitioning-based clustering method created by ensembling the k-means and k-modes clustering algorithms. To learn more about k-prototypes clustering, you can read this article on k-prototypes clustering with a numerical example. To read its python implementation, you can read this article on clustering mixed data types in python.
To read about how to use the elbow method with k-prototypes clustering, you can read this article on the elbow method to find the best k for k-prototypes clustering.
Conclusion
In this article, we have discussed the elbow method and its implementation in Python. Here, we discussed the elbow method for k-means and k-modes clustering algorithms. I have also provided the link to the article on the implementation of the elbow method for k-prototypes clustering in python. You can also refer to the article if you want to.
To explore data visualization, you can have a look at this article on how to avoid chart junk.
I hope you enjoyed reading this article. Stay tuned for more informative articles.
Happy Learning!
